Whether it’s choosing a life partner or the next restaurant you’re going to eat at, you need to make choices in life with imperfect information, and without knowing how different choices would have played out.
But what if I told you that mathematicians have cracked the code of life for us? What if I told you, they’ve figured out the optimal strategy that maximises our chances of selecting the best partner, job offer, house, etc. and even winning at Wordle (who’s to judge which one is more important)?
The theory of optimal stopping provides a strategy that literally minimises our regrets - i.e. how much worse our decision turns out to be compared to the best possible decision we could have made. Who you could have married if you continued to look for a partner vs. who you married, for instance.
And, of course, the theory of optimal stopping is also applicable to the world of B2B SaaS, which brings us to the second edition of “Math meets B2B SaaS”!
The first edition of "Math meets B2B SaaS" covered what waiting for a bus and crossing the chasm have in common, and how Poisson processes can help you think about your GTM strategy from a new perspective.
In this article, I’ll cover how you can leverage the optimal stopping theory to land on the best Ideal Customer Profile (ICP). Let’s dive in!
Back to basics: What’s even sequential decision making?
Sequential decision making is the process of making a series of decisions in a specific order, where the outcome of each decision affects the options available for the next decision. So, yes, pretty much how life works.
The optimal stopping theory is a special case of sequential decision making where
Our options (e.g. job offers, candidates, suitors, houses) arrive in a random order over time, and each time, we make a decision as to whether we like to continue to see other options (exploration*) or stop to make a decision (exploitation**).
Once we’ve made a decision, we can’t look ahead and see what else we could have selected.
And, similarly, we can’t go back in time and choose an option we previously passed on.
*Exploration refers to the process of gathering information and learning about different options or actions. This can include trying out different strategies or actions in order to determine their effectiveness. **Exploitation, on the other hand, refers to using the knowledge and information that has been gathered through exploration to make decisions and take actions that are likely to be the most beneficial.
Now that we’ve briefly covered the basics of sequential decision making, how is this relevant to B2B SaaS?
Let’s say that you’re on your journey to Product-Market Fit, and you’re trying to work out whose problem you’re solving best (or you’re on your journey to Go-To-Market Fit and you’re exploring where to expand into next).
You have a list of characteristics / external indicators that you think are likely to increase the chances of a company being interested in your product and becoming a customer. Companies sharing a set of these characteristics are called Customer Profiles.
Different Customer Profiles are likely to have different product value drivers, and require different Go-To-Market strategies.
So it’s not wise to go after multiple Customer Profiles at once (for more on this, check out Ingrid’s post).
Similarly, it’s not wise to deploy all your resources testing out a single Customer Profile for a long time, as the chances are the first Customer Profile you target is not the best one you could have settled on.
How do you maximise your chances of landing on the Ideal Customer Profile given the obvious time and capital constraints?
Case 1) If you test a very small number of Customer Profiles, then you don’t collect enough information to set the benchmark for what ‘success’ looks like; you risk exhausting your resources on a suboptimal Customer Profile.
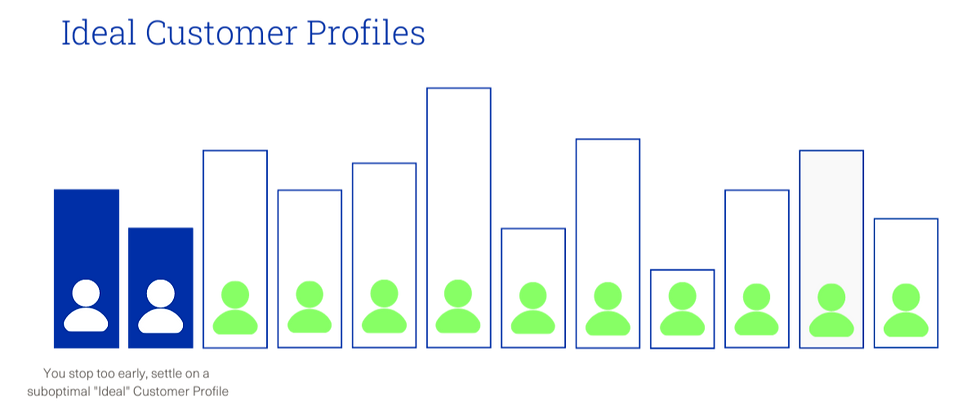
Case 2) If you keep searching for the Ideal Customer Profile, then you are likely looking for a Customer Profile that doesn’t exist; you will miss out on the opportunity to properly grow within your actual Ideal Customer Profile.
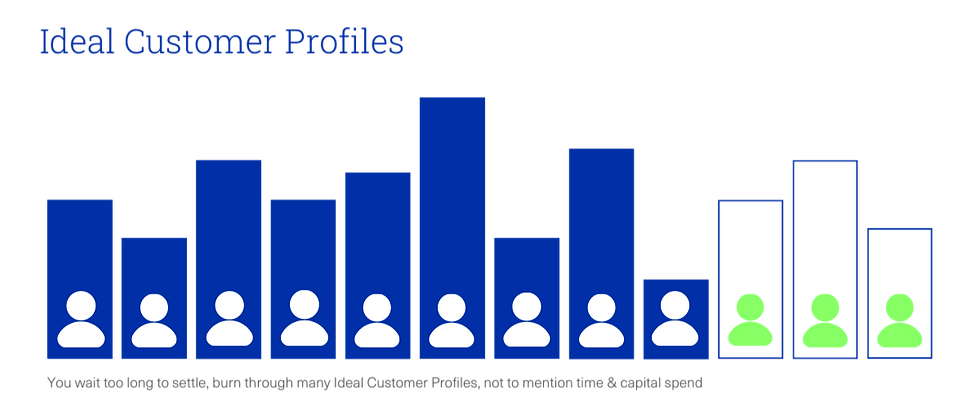
So how do you balance the tradeoff between
exploring different Customer Profiles and
settling on a Customer Profile to start showing consistent traction and getting ready for the next phase of growth?
When is the optimal time to switch from exploration to exploitation?
Well, lucky for us - it’s a solved problem!
Here are the maths for those who are interested:
And the answer is…
You should reject the initial 36.8% (1/e to be precise) of your Customer Profile pool (n), and select the next Customer Profile that is better than the initial 36.8%.
In other words, you should experiment with a third of the potential Ideal Customer Profiles, and then settle on the first Customer Profile that performs better than all the others.
At this stage, the question naturally becomes how do you determine what your n (total number of customer profiles) is. It’s your n because it’s going to depend on your company’s circumstances (business model, runway, stage, market positioning, to name a few).
But let’s think through an example:
Let’s say that you’re an SME software business looking to secure your next round of funding in 2 years’ time, and you want to have settled on your perfect ICP at least 6 months before that to have enough time to demonstrate healthy growth off the back of it. This gives you 18 months to settle on your ICP. If you can reach and test a new Customer Profile every 1.5 months, then your n becomes 18/1.5 = 12. For n = 12, r = 12 * 37% ≈ 4. This suggests you should reject the initial 4 Customer Profiles you explore and settle on the next one that performs better than the initial 4.
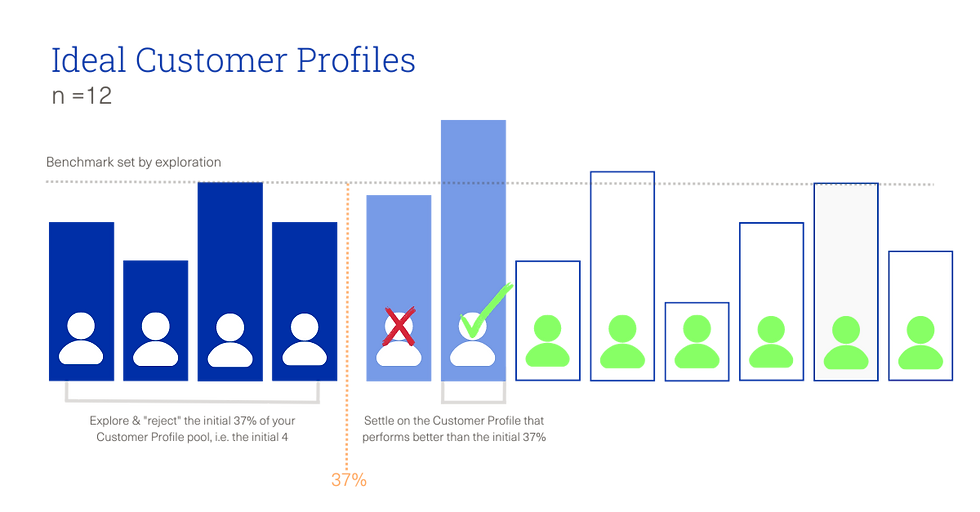
With the optimal stopping theory, the probability of success converges to 37%. So, this strategy increases your chances of settling on the perfect ICP from 8% (1/12 on random selection) to 37%!
The improvement is even greater for larger values of n (e.g. for n = 100, your chances increase from 1% to 37%).
But even for small values of n, this strategy is worth pursuing: if you were an enterprise software business with long sales cycles where testing different Customer Profiles would take longer and bring your n down to let’s say 3, applying the optimal stopping theory would still increase your chances of settling on the best ICP from 33% to 50%! 😎
(When n=3, r =1, so you always reject the first ICP that you explore, and then settle on the ICP that performs better than the first. To see how you achieve a 50% success rate, you can check out Lorenzo’s post where he clearly outlines the universe of possibilities and your chances of selecting the best option whilst always rejecting the first one, for n=3)
If you made it this far only to find out what the best strategy to win at Wordle is, you haven’t been forgotten! 🤓
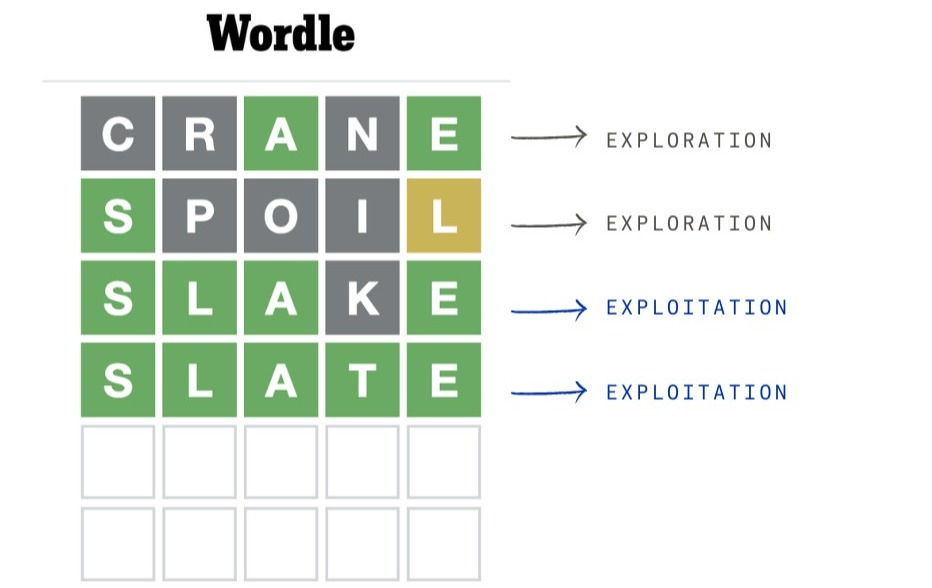
In Wordle our n = 6, which means our r = 2, so we should not try to guess (exploit) what the word of the day is, but instead try to hit as many different letters as possible (explore) with the first two guesses.
Not sure where the ‘Crane’ vs. ‘Slate’ debate eventually settled, but I'd chosen ‘Crane’ as my opening guess with no intention to actually guess the word of the day, but because it has as many different letters as a 5-letter word can.
For my second 'guess with no intention to guess', I chose ‘Spoil’ for the very same reason - to collect as much information as possible by testing 5 different letters.
I switched to exploitation in guess #3 as the initial 10 letters gave me enough information. And funny enough the word of the day turned out to be Slate!
P.S. The theory of optimal stopping can be applied to various business decisions, such as finding the perfect VP of Sales, office, or the next offsite location. (although agreeing on the ranking for the last one might be a long debate on its own!)
Intrigued to find out more about ‘stopping problems’? I highly recommend:
Mathematician Dr. Hanna Fry’s Ted talk: “The mathematics of love” where she talks about how to find the perfect partner using the optimal stopping theory.
Lorenzo Duso - Math-Based Decision Making: The Secretary Problem
The Reflective Educator - How I used mathematics to choose my next apartment
‘The secretary problem’ in Section 11.2 of Optimal Learning (or Penn Math).
For further information on Ideal Customer Profiles:
Oxx GTMF Toolkit - GTMF accelerators
Oxx GTMF FAQ - Target Segments
.png)


